本文简单讨论如何在服务端实现基于三角形网格的寻路算法。
地图表示
1. 基于路点
基于路点是最原始的寻路方案,比如要让你实现一个迷宫,你会很自然地想到用0代表通路,1代码障碍物,整个迷宫地图由0和1构成的点阵来表示。这就是基于路点,本质上是将地图上可以通过的位置(坐标状态)都记录下来。

2. 基于网格
基于网格是指对地图进行预处理,将地图边界拐点和障碍物外围拐点所形成的离散点集合转换为一个由多边形(通常是三角形)构成的网格,然后去掉障碍物内部的多边形,剩下即为所有可达地点的网格,称作寻路网格。或者换个角度来讲,将地图上的障碍物和边界之外去掉,然后将剩下的部分通过多边形切割,得到寻路网格。

以下简单对比基于路点和基于网格的寻路:
- 基于路点要比基于网格存储更多的信息
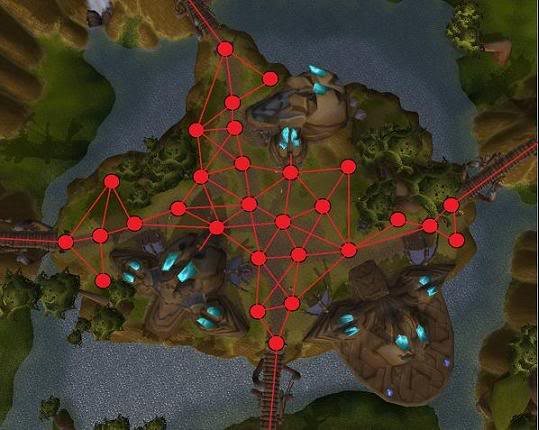

- 基于路点寻路,即使没有障碍物,也可能走折线
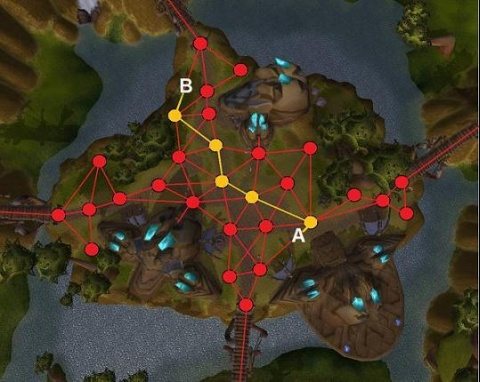
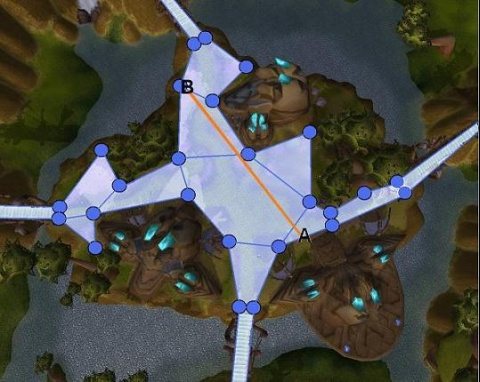
基于网格可以更好地处理平滑转弯,角色大小等细节,如体型过大的角色可能无法通过某个小通道
基于网格可以通过网格保存更多的地表信息,如水中移动速度更慢,可用于寻路算法计算权重
寻路算法
不管是基于网关还是基于路点,最终的地图都是图结构,只不过基于路点的图结构基本单位是点,而基于网格的基本单位是网格。基于路点的寻路比较简单,通常通过 A* 或 Dijkstra 算法即可直接算出。这里讨论基于三角形的网格寻路。
Step 1. 导出网格数据
网格地图需要对地图进行预处理生成地图元数据,这里不讨论生成过程,假设我们已经得到了地图元数据,其中包含地图上所有的三角形信息。
Step 2. 数据预处理
预处理有两个目的:
- 给定一个点,能快速找到其所在的三角形
- 给定一个三角形,能快速索引到与其相连的其它三角形
第一点可以通过将整个地图(假设为方形)组织成四叉树,起初所有的三角形都在根节点下,当节点下的三角形超过某个阈值时,将该节点进一步分为四个节点,各个节点保存其 Rect 区域内的所有三角形,那些在边界处的三角形(存在于多个 Rect 区域内),则继续挂在根节点上,这样在查找点时,可通过该点是否在节点区域内不断递归缩小查找范围,找到所在三角形。
如下图,我们将三角形网格地图分为了四部分,当我们要寻找 A 点所在的三角形时,只需遍历左上角黑线包围的三角形即可,在地图较大,四叉树层数较深时,能够极大优化三角形查找。
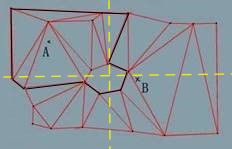
现在来解决如何存储三角形相邻关系,如果将三角形看做点,本质上我们要做的其实是要保存一张图,保存图的方式通常有邻接矩阵,邻接图等,一个地图可能有上万网格,而每个三角形相邻的三角形通常是个位数,在这种情况下,用邻接表是个不错的选择,具体的实现不再罗列,本质上该部分预处理数据提供网格的通路信息。
Step 3. 寻路
到这里我们开始阐述寻路的具体过程,我们有了以上的预处理数据,并且给定地图上的两个点 A,B,求 A, B 之间的寻路路径:
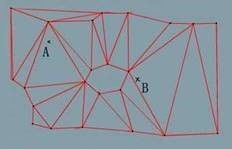
我们将寻路算法分为如下步骤:
3.1 找到 A, B 两点所在的三角形
基于前面我们创建的四叉树,我们可以得到 A,B 两点所在的三角形
3.2 找到两个三角形之间的最短三角形路径
前面提到,如果将三角形看做基本单位,那么我们的网格图本质上就是个无向图,基于图的寻路算法主要有 A* 和 Dijkstra 算法,通常启发式的 A* 是更好地选择,我们可以用三角形的中心点(三条边中线的交点)到目标三角形的中心点的距离作为启发函数 h值。
3.3 将三角形路径转换为最短线路径
假设我们现在得到了A,B 间的网格路径:
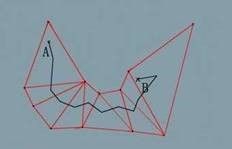
现在我们要将其转换为角色最终行走的线路径,一种简单的算法是直接将沿途三角形的中心点联结起来,得到如上图所示的线路,但一来是路线存在不必要的折现,不是最短线路。二来返回给客户端的点过多,不适合作为服务器寻路结果。理想的最短路线如下图所示:
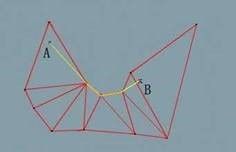
其中只有三个拐点,我们只需要将这三个拐点返回给客户端即可(这里不讨论平滑转弯)。接下来我们来尝试将网格路径推演为最短线路径。
首先我们知道,拐点必然出现在三角形路径上某两个三角形共同边的端点,因此我们尝试遍历三角形路径上所有的共同边,得到拐点。如上图所示,A,B 两点间一共有9条共同边,我们称这9条边为临边或者穿出边,我们以 A 点为起点,对第一条临边作两个向量:
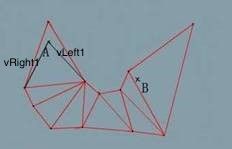
我们将这两个向量通过向量叉乘的方式分为左向量和右向量,设为 vLeft1,vRight1,我们可以非正式地将 vLeft1 和 vRight 1之间的夹角看做角色的当前视野(之后我们用{vLeft, vRight}表示)。然后对第二条临边做向量,vLeft2 和 vRight2,发现新视野{vLeft2,vRight2}在当前视野{vLeft1,vRight1}之间,因此更新当前视野为{vLeft1, vRight2}:
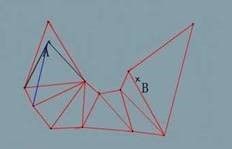
同样,继续从出发点对第三条临边锻炼做向量得到新视野 {vLeft3, vRight3},仍然在当前视野{vLeft1, vRight2}内,如此迭代:
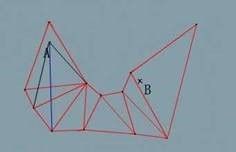
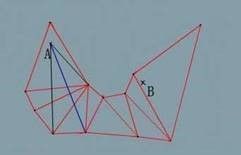
直到我们对第五条临边做向量得到的视野{vLeft4, vRight4},发现vRight4不在当前视野{vLeft1, vRight4}内,即视野不是包含关系:
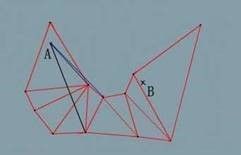
此时忽略第五条临边,当前视野不变,仍然是{vLeft1, vRight4},继续对第六条临边作视野:

发现新的视野{vLeft6, vRight6}在当前视野{vLeft1, vRight4}左侧,没有重叠部分,即 vLeft6 和 vRight6 均在 vLeft1 的左侧,换句话说,我们无法从起点直接到达第6条临边,需要在某个点转弯,这个点就是拐点,也就是这里的 Left1 的非起点端点。此时记录该拐点 C,将当前起点从 A 点更新到 C 点,重新找到与 C 点不相邻的第一条临边,也就是整条路径的第5条临边,重新初始化当前视野,递归寻找从 C 点到达 B 的路径拐点。

如此递归,直到找到最后一个拐点P:
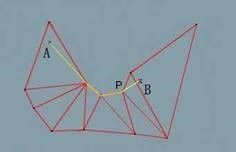
从 P 点的视野可以直接连到最后一个三角形,也就是与目标点B所在的三角形,由于 B 在 P 点的视野内,因此 P,B 可直接连线到达。如果 B 点不在 P 的视野内,则还需一个拐点,通常我们将目标点作为一条特殊的边来处理即可,即长度为0的边,这样可以用同样的拐点算法来计算。至此,我们就得到了 A, B 两点间的最短路径。
其它细节
到此我们就得到了基于拐点的寻路路径,本文只讨论了大概思路,实际上寻路还有很多有意思的问题值得探讨,如:
- 如何在寻路时考虑到单位的半径?Tips: 在寻路算法找出三角形路径时,比较三角形的临边和角色大小
- 如何在寻路时考虑到各种地形的权重?Tips: 将地形信息保存在三角形网格中,在 A* 算法的代价函数中考虑三角形权重
- 如何动态更新寻路?Tips: 可选方案: a. 定时检查 b. 每 N 步检查一次 c. 有障碍物时触发相关寻路更新 d. 寻路局部更新优化
由于懒且画工不好,本文图片均出自以下参考文章: