源自于我做的一次公司内部的技术分享,这是初稿。 PPT 就不贴了。
一. 序章: 可计算模型
1936 阿隆佐·邱奇发表可计算函数的第一份精确定义,即Lambda演算(λ演算)。λ演算是一套从数学逻辑中发展,以变量绑定和替换的规则,来研究函数如何抽象化定义、函数如何被应用以及递归的形式系统。
1936 艾伦·图灵提出图灵机设想,通过TAPE,HEAD,TABLE,STATE四个部分模拟人的纸笔运算
1945 冯·诺伊曼提出冯·诺伊曼结构(存储程序型电脑),是通用图灵机实现
1958 约翰·麦卡锡,发明了一种列表处理语言(Lisp),这种语言是一种阿隆佐lambda演算在现实世界的实现,而且它能在冯·诺伊曼计算机上运行
图灵机设想和 Lamdba 演算都是一种抽象计算模型,是解决可计算问题的一种方案,通俗来讲,就是将计算以数学的方式抽象化,以便证明和推导。图灵机和 Lamdba 演算这两个可计算理论已经被证明是等价的。
函数式的起源Lambda 演算甚至还要早于图灵机,但图灵机由于其更具实现意义,也更容易被理解,因此很早就有了硬件实现基础,而 Lambda 演算是一套更接近软件而非硬件的形式系统,Lambda 演算的第一台硬件则要等到1973年的 MIT 人工智能实验室开发的Lisp机。
二. 什么是函数式编程
函数式编程是一种编程范式,我们常见的编程范式有命令式编程,函数式编程,逻辑式编程,常见的面向对象编程和面向过程编程都是命令式编程。
命令式编程是面向计算机硬件的抽象,如变量(抽象存储单元),表达式(算数运算与内存读写),控制语句(跳转指令),最终得到一个冯诺依曼机的指令序列。
函数式编程的基础模型来源于λ演算,是阿隆佐思想的在现实世界中的实现。不过不是全部的lambda演算思想都可以运用到实际中,因为lambda演算在设计的时候就不是为了在各种现实世界中的限制下工作的(毕竟是数学家捣鼓出来的东西)。 目前的函数式编程语言基本都是翻译为冯诺依曼指令实现的。
三. 函数式编程概念
变量:
- 命令式: 代表存储可变状态的单元(内存地址),相当于地址的别名 x = x + 1
- 函数式: 代表数学函数中的变量,映射到某个值,相当于值的别名 2x = 4
函数:
- 命令式: 描述求解过程(怎么做),本质上是一系列的冯诺依曼机指令,can do anything
- 函数式: 数学概念里的函数,描述映射(计算)关系(做什么),也称为纯函数/无状态函数
四. 函数式编程特性
1. 不可变语义
比如我们有一个 Point类,其 moveBy 方法对 x,y 坐标进行偏移,得到新的 Point 对象:
// 命令式写法: 直接修改内存值
func (p *Point) moveBy(deltaX, deltaY int) {
p.x = p.x + deltaX
p.y = p.y + deltaX
}
// 函数式写法: 新建一个 Point 对象,函数本身只需关心对象的映射,而非对象复用等实现细节。在语义上,新旧 Point 代表完全独立并可不变的两个"Point 值"。
func moveBy(p *Point, deltaX, deltaY int) *Point {
return &Point{
x: p.x+deltaX,
y: p.y+deltaY,
}
}
没有可变状态,也就没有 for, while 循环,使得函数式编程严重依赖递归。
这里的不可变,指的是语义上的不可变,而非其底层实现上的不变。比如Erlang 虚拟机用 C 实现,通过写时拷贝来实现不可变语义,但针对比如binary 升级,Pid打包等,虽然底层的实现结构可能会改变,但对应用层来说语义是不变的。
2. 纯函数
- 确定性: 相同输入得到相同输出,函数的返回值和参数以外的其他隐藏信息或状态无关
- 无副作用: 函数不能有语义上可观察的副作用,诸如“触发事件”,使输出设备输出,或更改输出值以外对象的内容等
纯函数都是显式数据流的,即所有的输入都通过参数传入,所有输出都通过返回值传出。
纯函数即无状态函数,微服务中的无状态服务也有一个无状态似,但关注的是整个处理流程的无状态,即把状态往两边推到输入(如Network)和输出(DB,Cache,Log 等),这样服务能够横向扩展和动态伸缩(就像一个巨大的纯函数)。而对函数式而言,理论上演算过程中的任一处理步骤(每次函数调用)都是无状态的,因此可伸缩和并发的粒度更小。
在实现上,无状态和不可变语义一样,是语义上的,无状态是指函数本身不能有可以改变状态的指令,从系统层次上来看,要说绝对没状态是不可能的,比如调用函数会导致进程栈增长,页面换入换出等。另外,在 Haskell 语言中,还有惰性求值,会使得在执行纯函数时执行一些外部操作(比如文件 IO)。因此从这个角度来看,我们用命令式语言也可以实现无状态效果。
3. 递归与尾递归
递归在几乎所有命令式编程语言中都有,即函数调用自身,在函数式编程中,由于没有可变状态,for, while 循环都只能通过递归来实现,因此函数式编程严重依赖递归:
以阶乘为例:
// 自底向上,递推求解
func fact_1(n int) int {
acc := 1
for k:=1; k<=n; k++ {
acc = acc*k
}
return acc
}
// 自顶向下,递归求解
func fact_2(n int) int {
if n == 0 {
return 1
} else {
return fact_2(n-1)*n
}
}
// 自顶向下,递归求解 - Erlang
fact(N) when N == 0 -> 1;
fact(N) when N > 0 -> N*fact(N-1).
// 递归求解 - Erlang - 尾递归版
fact1(N) -> fact(1, N).
fact(Acc, N) when N == 0 -> Acc;
fact(Acc, N) when N > 0 -> fact(Acc*N, N-1).
我们知道在现代冯诺依曼结构计算机中,递归和普通函数一样,是通过函数调用栈来实现的,为了防止函数栈肆意扩展(导致栈溢出),通常函数式语言的编译器都会实现尾调用优化。尾调用是指一个函数里的最后一个动作是返回一个函数的调用结果的情形,即最后一步新调用的返回值直接被当前函数的返回结果。这种情况下,函数可以直接复用当前函数栈的栈空间执行尾调用,减少栈空间使用并提高效率。(尾递归是函数式基于命令式语言实现时的一个实现上的优化(栈空间是有限的),并非Lamda 演算本身的内容。)
递归是函数式中非常核心的一个概念,其在函数式语言中的低位要比在命令式语言高很多,理解递归是理解函数式的基础。递归是另一种我们思考和解决问题的方式,在一些情景下,使用递归会让问题简化许多。比如经典的找零钱问题:
// 若干面值钞票,给一张大面值货币要兑换成零钱,求有多少种兑换方式
// 递归版本
func countChange(money int, coins []int) int {
if money < 0 || len(coins) == 0 {
return 0
}
if money == 0 {
return 1
}
return countChange(money, coins[1:]) + countChange(money-coins[0], coins)
}
// 迭代版本
func countChange2(changes []int, money int) int {
n := len(changes)
dp := make([]int, money+1)
for i:=1; i<=money; i++ {
dp[i] = 0
}
dp[0] = 1
for i:=0; i<n; i++ {
for j:=changes[i]; j<=money; j++{
dp[j] += dp[j-changes[i]]
}
}
return dp[money]
}
可以看到,递归版比迭代版要容易理解得多,后者需要手动维护状态,而前者将状态隐藏到递归过程中了。类似的还有背包问题,都是理解递归很好的例子。
4. 惰性求值/乱序求值
表达式不在它被绑定到变量之后就立即求值,而是在该值被取用的时候求值。这篇文章 更详细地讨论了惰性求值。
A = dosomething1()
B = dosomething2(A)
C = dosomething3()
编译器很容易就可以推断出,A->B 和 C 可以乱序(无状态)或者并行(不可变语义)执行,并且对 A,B,C 的求值可以等到它们被引用的时候再计算,因此函数式本身的优化空间是比较大的。
5. 柯里化(currying)
柯里化:将一个多参数函数分解成多个单参数函数,然后将单参函数多层封装起来,每层函数都返回一个函数去接收下一个参数,这可以简化函数的多个参数。比如前面我们的尾递归版阶乘计算,可以写成:
fact2(Acc) ->
fun(N) -> fact(Acc, N) end.
F = fact2(1)
F(10)
换成 Lua 可能更容易理解,比如我们有两个参数的 add :
add = function(x, y)
return x + y
end
print(add(3,4))
可将其柯里化为:
add = function(x)
return function(y)
return x + y
end
end
print(add(3)(4))
上面我们列举的柯里化看起来很像Lua,Go等语言中的闭包(词法闭包,Lexical Closure),实际上柯里化是Lambda 演算中的概念,用于简化推导流程。闭包只是一种实现方式,如C++ STL 的bind1st和bind2nd也可以实现固化函数参数的作用。
柯里化所要表达是:如果你固定某些参数,你将得到接受余下参数的一个函数,所以对于有两个变量的函数x+y,如果固定了x=3,则得到有一个变量的函数3+y(是不是很像多项式一个一个变量求解)。这就是求值策略中的部分求值策略。柯里化具有延迟计算、参数复用、动态生成函数的作用。
6. 高阶函数
函数式的要义之一就是将函数当做普通对象一样,可以被当做参数传递,也可以作为函数返回值(在λ演算创始人阿隆佐·邱奇的眼里,一切且函数,变量也是函数)。所谓高阶函数就是以函数为参数或返回值的函数,有了高阶函数,就可以将复用的粒度降至函数级别,相对面向对象而言,复用粒度更低。
sumInts(A, B) when A > B -> 0;
sumInts(A, B) -> A + sumInts(A+1, B).
sumFacts(A, B) when A > B -> 0;
sumFacts(A, B) -> fact1(A) + sumFacts(A+1, B).
sum(F, A, B) when A > B -> 0;
sum(F, A, B) -> F(A) + sum(F, A+1, B).
> sum(fun fact1/1, 3, 6)
函数式语言通常提供了非常强大的”集合类”,可以基于高阶函数提供便捷的集合操作:
37> L = [1,2,3].
[1,2,3]
38> lists:map(fun(E) -> 2*E end, L).
[2,4,6]
39> lists:foldl(fun(E, Acc) -> Acc+E end, 0, L).
6
得益于函数式的无状态和不可变语义,将lists:map 函数改写为并发执行的 map 只需几十行代码,安全无副作用。
可能接触过面向对象编程的人都接触或使用过设计模式,在函数式编程里面,通过 function 实现设计模式要比 class, interface 那一套要简洁灵活得多。比如lists:map本身就是一个很好用的访问者模式。
7. Monad
前面提到,函数式中变量不可变,且纯函数没有副作用,那么函数式如何处理可变状态比如 IO 呢,在 Erlang 里,IO 通过 C 实现,即引入了可变性和副作用,并且 Erlang没有对这种副作用代码和纯代码分隔开,这得依靠程序员来做。而纯函数式语言 Haskell 采用了另一种方案: Monad。
单子(Monad)是来自范畴论中的概念,范畴论是数学的一门学科,以抽象的方法来处理数学概念,将这些概念形式化成一组组的“对象”及“态射”。
Monad 的概念被引入到 Haskell,表示”注入”和”提取”的概念,用于处理 IO,串联函数等。
Haskell严格地把纯代码从那些有副作用的代码(如 IO)中分隔开。就是说,它给纯代码提供了完全的副作用隔离。除了帮助程序员推断他们自己代码的正确性,它还使编译器可以自动采取优化和并行化成为可能。而 Monad 加上 Haskell 的类型类即成为分离纯函数和副作用函数的利器:
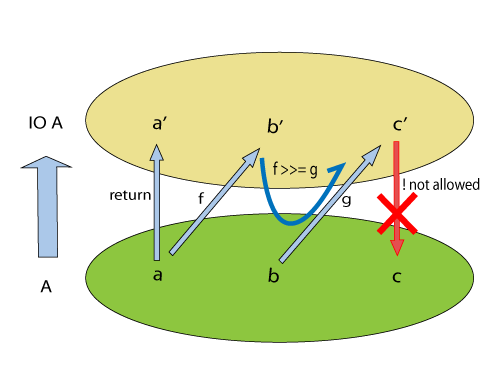
上图说明了 Haskell 如何通过 Monad 管理纯函数副作用函数。具体到代码,看起来像是这样:
name2reply :: String -> String
name2reply name =
"Pleased to meet you, " ++ name ++ ".\n" ++
"Your name contains " ++ charcount ++ " characters."
where charcount = show (length name)
main :: IO ()
main = do
putStrLn "Greetings once again. What is your name?"
inpStr <- getLine
let outStr = name2reply inpStr
putStrLn outStr
Haskell在纯代码和I/O动作之间做了很明确的区分。很多语言没有这种区分。 在C或者Java(包括 Erlang)这样的语言中,编译器不能保证一个函数对于同样的参数总是返回同样的结果,或者保证函数没有副作用。程序中的很多错误都是由意料之外的副作用造成的。做好这种隔离有利于程序员和编译器更好地思考和优化程序。
五. 函数式的优缺点
- 并发性: 函数无副作用(天然可重入),原生并发友好
- 确定性: 可读性高,易于测试和调试,错误易于重现
- 没有锁和指针就没有伤害
- 具有很大的优化潜力,如惰性求值,并发,缓存函数计算结果等,很多原本需要程序来做的事情,都可以由编译器来做。比如动态规划的缓存,MapReduce 等。
缺点:
- 处理可变状态如 IO 的能力弱(要么使用可变状态,要么使用 Monad)
- 为了维持不可变性,拷贝的开销
- 运行效率,依靠并发
六. 函数式的实现
1. Erlang
Erlang 不是一门纯函数式语言(提供了外部可变状态组件,如进程字典,Ets),但它充分利用函数式的无状态和不可变语义,将函数式的各种优势很好地利用了起来。Erlang 的具体介绍和细节我们就谈了,我着重讲一下其三个让其它语言”眼红”的三个特性:
高并发
Erlang 是 Actor 模型,一个 Actor 即一个 Erlang 进程,创建一个进程是微秒级的。Erlang 可以说是最早支持协程的语言之一,Actor 与 Actor 之间通过消息交互,加上不可变语义,使得 Erlang 比其它语言更易于实现安全的并发(Erlang/OTP并发编程实践作者将共享内存比作这个时代的goto)。
热更新
说起代码热替换,估计没有语言比 Erlang 做得更好了,这是 Erlang 的黑科技,一个用了你就回不去的功能。热更新对于游戏服务器的意义是很大的,游戏开发版本更新快,有时候有些不大不小的问题(比如一些调试日志忘删除了,某个小功能可能无法使用),通过重启来解决的代价太大(用户流失),用 Erlang 直接无缝热更,比无缝重启要方便快捷太多。
热更新的原理是代码版本替换,一方面仰仗于Erlang运行时的代码加载机制,另一方面,函数式也功不可没,一个具有内部状态的函数是很难做热更新的。
容错性
Erlang 有一个很有意思的slogan,叫”let it crash”,这看起来与命令式编程中的”defensive coding(防御式编程)”背道而驰,在大型分布式程序的构建过程中,代码会遇到各种各样的异常,代码编写者不可能或者说很难预料并且处理到所有的异常,在这个背景下,Erlang 提出”let it crash” 的概念: 既然未预料的异常无可避免,那么就应该统一隔离处理并且恢复它,注意,这里提到了三个词: 错误隔离,错误处理和故障恢复,大部分语言最多做到第一步(比如 Go 语言),而 Erlang 把整个三步都做到了虚拟机中。一个进程挂了,会由监督者发现,并且根据重启策略重启。 Actor 的状态隔离与轻量为整个容错性提供基础保障。
总的来说,Erlang 在并发,健壮性,可伸缩性方面,都有非常出色的表现。适用于 IO 密集型的软实时系统(设计之初就是为了解决电信通信问题的)。
2. Haskell
Erlang并不是一门纯函数式语言的话,进程字典,ets,IO 等状态性和副作用,Haskell 则剑走偏锋,号称是纯函数式语言。Haskell 我只看了一部分,以下是一些基础特性:
- 支持惰性求值
- 更彻底的函数(+,-)
- 静态类型系统 + 类型推导 + 强大的typeclass (==, Functor),支持自定义类
- 原生柯里化(
map (+1) [1,2,3]) - 引入范畴论的 Monad
七. 最后
1. 为什么函数式没有崛起?
图灵机是一个具备实现意义的 model,或者换句话说,lambda 演算则是更抽象,更上层的计算模型,图灵机也更符合人解决问题的方式(纸笔推演),更容易被没有数学背景的工程师所理解,因此很快在现实世界中实现推广。
一个有意思的论题是Worse Is Better,由 Common Lisp 专家Richard P. Gabriel在90年代反思 Lisp 这么牛的语言却日渐式微提出的观点,他提出软件设计有以下四大目标: 简单性,正确性,一致性,完整性
- 函数式语言: 正确性 = 一致性 > 完整性 > 简单(为了接口简单,宁愿实现复杂)
- 命令式语言: 简单性(实现简单优于接口简单)> 正确性 > 完整性 > 一致性
原文 Worse Is Better 中的 Worse 是指C/Unix将其简单性优于其它目标的做法(在作者看来是糟糕的),Better 是指 C/Unix 当下的处境(当然是非常流行),因此可以粗略理解为”简单的就是好的”。作者将C/Unix 的流行归功于他们实现简单,使得其像”病毒”一样可快速移植到与传播,用户也更愿意接受,等到用户产生依赖,再逐步完善。
当然,可能还有一个原因,那个年代计算机是稀缺资源,比较注重效率,而在冯诺依曼机上的实现的函数式语言自然没有早期的命令式语言快,自然也让 C,C+这类”简单粗暴”的语言飞速推广。再借助 OS,编译器等形成生态。
2. 函数式近几年开始受到更多的关注
由于软件复杂度和 CPU 核数的增加,多线程和其他形式的并行化变得越来越普遍, 管理全局副作用变得越来越困难,函数式的好处(正确性和一致性)开始体现出来,几十年前写的 Erlang 代码放到今天,无需任何改动,核数越多,跑得越快,因此现在的软件设计理念都会从函数式思想中学习一些东西。
从设计上来讲,现代语言都或多或少吸收了函数式的一些特性: 如function,闭包,尾递归,高阶函数等等。从理念上来讲,函数式的无状态为并发提供了另一种解决方案,比如近几年推崇的无状态服务设计,Erlang 的 Actor 模型等。
如今很多语言都支持多种编程范式,一些函数式语言也有可变状态,一些命令式语言支持部分函数式特性,理解函数式可以扩展我们解决问题的思路,找到更简洁有效的解决方案,如递归而不是迭代,函数注入而不是对象注入等。最后,我认为每个程序员都可以去学习一门函数式语言,扩展自己的思维,写出更灵活,安全,”纯洁”的代码。
参考:
Haskell: